Evaluating Square Roots
When the square root of a number is squared, the result is the original number. Since , the square root of is . The square root function is the inverse of the squaring function just as subtraction is the inverse of addition. To undo squaring, we take the square root. In general terms, if is a positive real number, then the square root of is a number that, when multiplied by itself, gives . The square root could be positive or negative because multiplying two negative numbers gives a positive number. The principal square root is the nonnegative number that when multiplied by itself equals . The square root obtained using a calculator is the principal square root. The principal square root of is written as . The symbol is called a radical, the term under the symbol is called the radicand, and the entire expression is called a radical expression.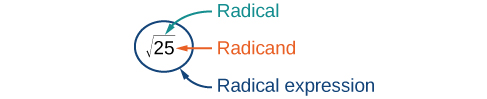
A General Note: Principal Square Root
The principal square root of is the nonnegative number that, when multiplied by itself, equals . It is written as a radical expression, with a symbol called a radical over the term called the radicand: .Q & A
Does ?
No. Although both and are , the radical symbol implies only a nonnegative root, the principal square root. The principal square root of 25 is .Example 1: Evaluating Square Roots
Evaluate each expression.Solution
- because
- because and
- because
- because and
Q & A
For , can we find the square roots before adding?
No. . This is not equivalent to . The order of operations requires us to add the terms in the radicand before finding the square root.Try It 1
Evaluate each expression.a. b. c. d.
Solution